LeetCode의 261번째 문제인 Graph Valid Tree를 함께 풀어보도록 하겠습니다.

이 문제는 LeetCode에서 유료 구독자만 접근할 수 있습니다. LintCode의 178번째 문제가 거의 동일하며 무료로 푸실 수 있으니 참고 바랍니다.

문제

주어진 n개의 노드에 0부터 n - 1까지 레이블이 붙은 그래프가 있습니다. 정수 n과 간선 목록이 주어지는데, 여기서 edges[i] = [ai, bi]는 그래프에서 노드 ai와 bi 사이에 무방향 간선이 있음을 나타냅니다.

주어진 그래프의 간선들이 유효한 트리를 이룬다면 true를 반환하고, 그렇지 않으면 false를 반환합니다.”

예제 1

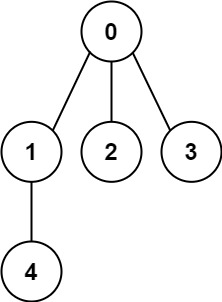
입력: n = 5, edges = [[0,1],[0,2],[0,3],[1,4]]
출력: true

예제 2

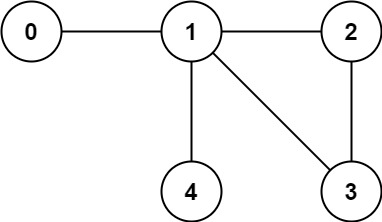
입력: n = 5, edges = [[0,1],[1,2],[2,3],[1,3],[1,4]]
출력: false

풀이 1

문제어서 유효한 트리가 무엇인지 대해서 정확히 언급이 되어 있지 않은데요. 먼저 그래프가 어떤 조건을 만족해야하는지 유효한 트리가 될 수 있는지 알아야 합니다.

그래프가 트리가 되려면 다음 두 가지 조건을 만족해야 합니다.

• 완전히 연결된(fully connected) 그래프여야 합니다. 즉, 어느 노드에서 시작하든 간선을 따라서 전체 그래프를 탐색할 수 있어야 합니다.
• 그래프에 순환(cycle)하는 부분이 없어야 합니다. 즉, 그래프 탐색 도중에 동일한 노드로 다시 돌아와서는 안 됩니다.

이 두 가지 조건을 만족하려면 그래프 탐색을 하면서 순환하지 않고 모든 노드를 방문할 수 있는지를 확인해야 합니다. 그래프에 순환하는 부분이 나오면 탐색을 중단하고 바로 유효하지 않은 트리라고 판단할 수 있으며, 탐색이 끝나면 여태까지 방문한 노드의 수가 입력 노드의 수와 일치하는지 확인해야합니다. 만약에 방문한 노드의 수가 더 작다면 완전히 연결된 그래프가 아니라는 뜻이기 때문입니다.

그래프를 탐색할 때 한 가지 조심할 부분은 주어진 그래프가 무방향(undirected) 그래프라는 점입니다. 무방향 그래프는 노드 간이 간선이 상호 쌍방으로 있기 때문에 간선이 끝나는 노드에서 다시 간선이 시작하는 노드로 돌아가지 않도록 주의해야하는데요. 재귀 함수의 인자로 간선이 끝나는 노드 뿐만 아니라 간선이 시작하는 노드까지 넘기면 어렵지 않게 간선이 시작하는 노드를 무시할 수 있습니다.

그럼 재귀 알고리즘을 사용하여 깊이 우선 탐색을 구현해보겠습니다.

class Solution:
    def validTree(self, n: int, edges: List[List[int]]) -> bool:
        graph = [[] for _ in range(n)]
        for node, adj in edges:
            graph[node].append(adj)
            graph[adj].append(node)

        visited = set()

        def has_cycle(node, prev):
            if node in visited:
                return True
            visited.add(node)
            for adj in graph[node]:
                if adj == prev:
                    continue
                if has_cycle(adj, node):
                    return True
            return False

        if has_cycle(0, -1):
            return False
        return len(visited) == n

참고로 파이썬의 any() 함수를 사용하면 인접 노드를 상대로 루프를 도는 코드를 더 간결하게 짤 수 있습니다.

class Solution:
    def validTree(self, n: int, edges: List[List[int]]) -> bool:
        graph = [[] for _ in range(n)]
        for node, adj in edges:
            graph[node].append(adj)
            graph[adj].append(node)

        visited = set()

        def has_cycle(node, prev):
            if node in visited:
                return True
            visited.add(node)
            return any(has_cycle(adj, node) for adj in graph[node] if adj != prev)

        if has_cycle(0, -1):
            return False
        return len(visited) == n

노드의 개수를 n, 간선의 개수를 e라고 했을 때, 이 풀이의 시간 복잡도와 공간 복잡도는 모두 O(n + e)입니다. 인접 리스트가 차지하는 메모리는 노드의 개수와 간선의 개수를 더한 것에 비례해서 커지며, 그래프 탐색에는 일반적으로 O(n + e) 시간이 소모되기 때문입니다.

풀이 2

간선의 수가 노드의 수를 비교하면 좀 더 간단히 그래프가 유효한 트리인지 알아낼 수 있습니다. 유효한 트리는 간선의 수가 노드의 수보다 항상 하나가 작기 때문입니다.

간선의 수 = 노드의 수 - 1

만약에 간선의 수가 노드의 수에서 1을 뺀 것보다 작다면 완전히 연결된 그래프일 수가 없습니다. 반면에 간선의 수가 노드의 수에서 1을 뺀 것보다 크다면 그래프에 순환이 있을 수 밖에 없습니다.

이 공식을 활용해서 애초에 완전히 연결되어 있지 않거나 순환이 있는 그래프를 걸러내면, 이런 부분에 대해서 신경쓰지 않고 단순히 그래프 내의 모든 노드를 방문할 수 있습니다.

이 알고리즘을 코드로 구현해보겠습니다.

class Solution:
    def validTree(self, n: int, edges: List[List[int]]) -> bool:
        if len(edges) != n - 1:
            return False

        graph = [[] for _ in range(n)]
        for node, adj in edges:
            graph[node].append(adj)
            graph[adj].append(node)

        visited = set()

        def dfs(node):
            visited.add(node)
            for adj in graph[node]:
                if adj not in visited:
                    dfs(adj)

        dfs(0)
        return len(visited) == n

이 풀이의 시간 복잡도와 공간 복잡도는 모두 O(n)이 되는데요. 간선의 수가 노드의 수에서 1을 뺀 것과 일치하는 그래프를 상대로만 깊이 우선 탐색을 하기 때문에, 항상 e = n - 1이 되고, 결국 e는 n에 비례하기 때문입니다.