LeetCode의 323번째 문제인 Number of Connected Components in an Undirected Graph를 함께 풀어보도록 하겠습니다.
이 문제는 LeetCode에서 유료 구독자만 접근할 수 있습니다. LintCode의 3651번째 문제가 거의 동일하며 무료로 푸실 수 있으니 참고 바랍니다.
문제
n개의 노드로 구성된 그래프가 있습니다.
정수 n과 배열 edges가 주어지는데, edges[i] = [ai, bi]는 그래프에서 ai와 bi 사이에 간선이 있음을 나타냅니다.
그래프 내의 연결된 구성 요소의 수를 반환하시오.
예제 1
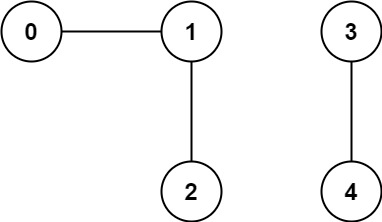
입력: n = 5, edges = [[0,1],[1,2],[3,4]]
출력: 2
예제 2
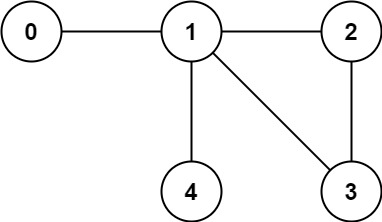
입력: n = 5, edges = [[0,1],[1,2],[2,3],[3,4]]
출력: 1
풀이 1: DFS (재귀)
문제에서 구성 요소란 그래프 내에서 서로 간선을 통해 연결되어 있는 노드의 무리를 의미합니다.
노드가 서로 하나도 연결되어 있지 않다면 구성 요소의 개수가 n이 되고, 반대로 모든 노드가 연결되어 있다면 구성 요소의 개수는 1이 될 것입니다.
각각의 구성 요소에 얼마나 많은 노드가 있는지는 해당 무리 안에 연결되어 있는 모든 노드를 탐색할 때 까지는 알 수 없겠죠? 따라서, 주어진 그래프를 깊이 우선 탐색하든 너비 우선 탐색하는 지는 별로 중요하지 않을 것입니다.
오히려 중요한 것은 탐색할 때 한 번 방문한 노드는 다시 방문하지 말아야 한다는 것인데요. 무방향(undirected) 그래프가 주어지기 때문에 노드 간에 쌍방으로 간선이 있어서 하나의 노드를 두 번 이상 방문할 수 있기 되기 때문입니다.
같은 노드의 중복 방문을 방지하기 위해서 안성맞춤인 자료구조가 있죠? 네, 바로 집합(Set)입니다. 그래프를 탐색하면서 집합에 방문한 노드를 저장해놓으면 재방문 되는 노드를 효과적으로 건널뛸 수 있습니다.
첫 번째 예제를 가지고 중복 방문에 주의하면서 깊이 우선 탐색을 같이 해볼까요?
우선 노드 0부터 그래프 탐색을 시작해보겠습니다.
무리의 개수를 하나 증가 시키고, 노드 0을 세트에 넣습니다.
무리 개수: 0 + 1 = 1
0
방문 노드: {0}
노드 0에는 노드 1이 연결되어 있습니다.
따라서 노드 1은 노드 0과 같은 무리에 속하므로 무리의 개수는 증가할 필요 없습니다.
노드 1은 세트에 넣어야 합니다.
무리 개수: 1
0 → 1
방문 노드: {0, 1}
노드 1에는 노드 2가 연결되어 있습니다.
따라서 노드 2은 노드 0, 노드 1과 같은 무리에 속하므로 무리의 개수는 그대로 입니다.
노드 2도 세트에 넣어야 합니다.
무리 개수: 1
0 → 1
↓
2
방문 노드: {0, 1, 2}
노드 2에는 아직까지 방문하지 않은 연결된 노드가 없으므로 다른 노드에서 또 그래프 탐색을 시작해야합니다.
노드 0, 노드 1, 노드 2는 아미 방문을 했으므로 노드 3에서 탐색을 시작합니다.
여기서 무리의 개수를 하나 증가 시키고, 노드 3을 세트에 넣어야합니다.
무리 개수: 1 + 1 = 2
0 → 1 3
↓
2
방문 노드: {0, 1, 2, 3}
노드 3에는 노드 4가 연결되어 있습니다.
따라서 노드 4은 노드 3과 같은 무리에 속하므로 무리의 개수는 변함이 없습니다.
노드 4도 세트에 넣어야 합니다.
무리 개수: 2
0 → 1 3
↓ ↓
2 4
방문 노드: {0, 1, 2, 3, 4}
더 이상 방문하지 않은 노드가 없으므로 그래프 탐색을 끝낼 수 있습니다.
최종 무리의 개수는 2가 됩니다.
이 깊이 우선 탐색 알고리즘을 재귀 함수를 이용하여 파이썬으로 구현해보겠습니다. 각 노드에 연결된 모든 이웃 노드를 상대로 루프를 돌기 적합하도록 입력 배열을 인접 리스트(adjacency list)로 변경하였습니다.
class Solution:
def countComponents(self, n: int, edges: List[List[int]]) -> int:
graph = [[] for _ in range(n)]
for node, adj in edges:
graph[node].append(adj)
graph[adj].append(node)
visited = set()
def dfs(node):
visited.add(node)
for adj in graph[node]:
if adj not in visited:
dfs(adj)
cnt = 0
for node in range(n):
if node not in visited:
cnt += 1
dfs(node)
return cnt
노드의 개수를 n, 간선의 개수를 e라고 했을 때, 이 풀이의 시간 복잡도는 O(n + e)입니다.
노드의 개수와 간선의 수를 합친만큼 재귀 함수를 호출해야하기 때문입니다.
공간 복잡도도 O(n + e)인데요.
인접 리스트의 크기가 노드와 간선의 수의 합에 비례하고 집합에 최대 n개의 숫자를 저장해야 하기 때문입니다.
풀이 2: DFS (스택)
면접관이 반복 알고리즘을 더 선호하신다면 스택(Stack) 자료구조를 사용해서 깊이 우선 탐색을 할 수도 있습니다.
class Solution:
def countComponents(self, n: int, edges: List[List[int]]) -> int:
graph = [[] for _ in range(n)]
for node, adj in edges:
graph[node].append(adj)
graph[adj].append(node)
cnt = 0
visited = set()
for node in range(n):
if node in visited:
continue
cnt += 1
stack = [node]
while stack:
node = stack.pop()
visited.add(node)
for adj in graph[node]:
if adj not in visited:
stack.append(adj)
return cnt
풀이 3: BFS (큐)
제가 맨 처음에 설명드릴 때 깊이 우선 탐색을 하든 너비 우선 탐색을 하든 무방하다고 말씀드렸죠? 이번에는 큐(Queue) 자료구조를 사용해서 너비 우선 탐색으로 구현해보겠습니다.
from collections import deque
class Solution:
def countComponents(self, n: int, edges: List[List[int]]) -> int:
graph = [[] for _ in range(n)]
for node, adj in edges:
graph[node].append(adj)
graph[adj].append(node)
cnt = 0
visited = set()
for node in range(n):
if node in visited:
continue
cnt += 1
queue = deque([node])
while queue:
node = queue.pop()
visited.add(node)
for adj in graph[node]:
if adj not in visited:
queue.append(adj)
return cnt
마치면서
코딩 시험에서 그래프(Graph)을 다루는 유형의 문제에서는 이 문제가 가장 기본이 된다고 볼 수 있는데요. 본 문제를 통해 기본기를 잘 닦아놓으셔서 같은 유형의 좀 더 어려운 문제를 풀 때 큰 도움이 되었으면 좋겠습니다.
코딩 테스트에서 그래프 자료구조를 어떻게 다루는지에 대해서 더 공부하고 싶으시다면 관련 게시물을 참고 바랄께요.