LeetCode의 297번째 문제인 Serialize and Deserialize Binary Tree를 함께 풀어보도록 하겠습니다.
문제
직렬화는 데이터 구조나 객체를 비트 시퀀스로 변환하여 파일이나 메모리 버퍼에 저장하거나 네트워크 연결을 통해 전송하여 나중에 동일한 컴퓨터 환경이나 다른 컴퓨터 환경에서 다시 복원할 수 있도록 하는 과정입니다.
이진 트리를 직렬화하고 역직렬화하는 알고리즘을 설계하십시오. 직렬화/역직렬화 알고리즘의 작동 방식에 대한 제한은 없습니다. 단지 이진 트리가 문자열로 직렬화되어 이 문자열을 원래의 트리 구조로 역직렬화할 수 있어야 합니다.
입력/출력 형식은 LeetCode가 이진 트리를 직렬화하는 방식과 동일합니다. 이 형식을 따를 필요는 없으므로 창의적이며 다른 접근 방법을 스스로 고안해야 합니다.
예제
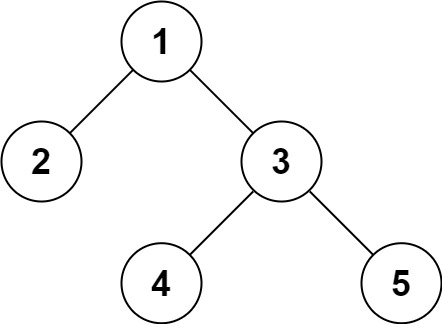
입력: root = [1,2,3,null,null,4,5]
출력: [1,2,3,null,null,4,5]
입력: root = []
출력: []
풀이 1
우선 LeetCode가 보통 어떻게 이진 트리를 직렬화하는지 살펴볼까요?
예를 들어, 첫 번째 예제에서 주어진 트리는 다음과 같은 모습인데요.
1
/ \
2 3
/ \ / \
N N 4 5
/ \ / \
N N N N
입력을 보면 다음과 같이 배열의 형태로 직렬화가 되어 있다는 것을 알 수 있습니다.
[1,2,3,null,null,4,5]
글자의 순서를 보면 깊이 우선 탐색(DFS)을 했다는 것을 알 수 있습니다. DFS 중에서도 부모 노드를 먼저 방문하고 좌측 자식 트리, 우측 자식 트리 순으로 방문하는 전위 순회(pre-order) 방식입니다.
트리를 순회하는 방법에 대해서는 별도의 글에서 자세히 설명하고 있으니 참고하세요.
그런데 우리는 배열이 아닌 문자열의 형태로 직렬화를 해야하기 때문에, 동일하게 전위 순회 방식으로 직렬화하면 다음과 같은 문자열을 얻을 수 있을 것입니다.
null도 문자를 바꿔야 해서 간단하게 글자 N으로 표시하였습니다.
1,2,N,N,3,4,N,N,5,N,N
만약에 이렇게 직렬화를 한다면 본래 모습의 트리로 역직렬화가 가능할까요? 똑같이 전위 순회 방식으로 문자열 내의 글자를 순서대로 하나씩 처리해보겠습니다.
전위 순회를 했기 때문에 첫 번째 글자가 트리의 최상위 노드라는 것은 의심의 여지가 없습니다.
1,2,N,N,3,4,N,N,5,N,N
^
1
/ \
1,2,N,N,3,4,N,N,5,N,N
^
우측 자식 트리보다 좌측 자식 트리를 먼저 방문했으므로, 두 번째 글자는 최상위 노드의 좌측 자식을 일 것입니다.
1
/ \
2
그 다음 글자는 N인데요. 이 것은 노드 2에 좌측 자식이 없다는 뜻입니다.
따라서 우리는 더 이상 좌측 자식 경로를 따라서는 내려갈 수 없습니다.
그런데 그 다음 글자도 N입니다. 이 것은 노드 2의 우측 자식도 없다는 뜻이겠죠?
따라서 우리는 더 이상 우측 자식 경로를 따라서도 내려갈 수 없습니다.
1,2,N,N,3,4,N,N,5,N,N
^ ^
1
/ \
2
/ \
N N
노드 2에 대한 탐색을 마쳤으므로 부모인 노드 1로 다시 돌아옵니다.
다음 글자 3은 노드 1의 우측 자식 노드가 될 것입니다.
1,2,N,N,3,4,N,N,5,N,N
^
1
/ \
2 3
/ \ / \
N N
이제 노드 3의 좌측 노드가 나올 차례인데 글자가 4입니다.
1,2,N,N,3,4,N,N,5,N,N
^
1
/ \
2 3
/ \ / \
N N 4
/ \
1,2,N,N,3,4,N,N,5,N,N
^ ^
이제 노드 4의 좌측 노드가 나올 차례인데 글자가 N입니다.
이 경로로는 더 이상 내려갈 수 없어서 다음 글자를 보니 또 N입니다.
따라서 노드 4는 자식이 없다는 것을 알 수 있습니다.
1
/ \
2 3
/ \ / \
N N 4
/ \
N N
노드 3으로 올라와서 다음 글자를 보면 5입니다.
글자 5는 노드 3의 우측 자식 노드가 되야 합니다.
1,2,N,N,3,4,N,N,5,N,N
^
1
/ \
2 3
/ \ / \
N N 4 5
/ \ / \
N N
다시 한 번 글자 N이 연속으로 두 번 나왔습니다.
이 말은 노드 5도 자식이 없다는 뜻입니다.
1,2,N,N,3,4,N,N,5,N,N
^ ^
1
/ \
2 3
/ \ / \
N N 4 5
/ \ / \
N N N N
입력 트리의 모습을 그대로 복원하게 되었습니다. 🎉
가장 중요한 부분은 글자 N을 만나면 해당 경로의 탐색을 중단하고 부모 노드로 돌아오는 것입니다.
그럼 지금까지 설명드린 알고리즘을 코드로 구현해보겠습니다.
serialize() 메서드는 전형적인 전위 순회 구현 기법을 따라서 특별할 것은 없는데요.
deserialize() 메서드의 경우 조금 더 복잡한데요.
우선 문자열을 ,를 기준으로 쪼개서 배열에 저장해줘야 하고요.
그리고 재귀 함수 외부에서 변수를 하나 선언하여 현재 글자를 기리키는 인덱스를 저장합니다.
그 다음 재귀 함수 내부에서 트리 노드를 생성하거나 글자 N을 만났을 때 1씩 증가시켜줍니다.
class Codec:
def serialize(self, root):
if not root:
return "N"
left = self.serialize(root.left)
right = self.serialize(root.right)
return f"{root.val},{left},{right}"
def deserialize(self, data):
values = data.split(",")
idx = 0
def dfs():
nonlocal idx
if values[idx] == "N":
idx += 1
return None
node = TreeNode(int(values[idx]))
idx += 1
node.left = dfs()
node.right = dfs()
return node
return dfs()
트리의 노드 개수를 n이라고 했을 때, 이 풀이의 시간 복잡도와 공간 복잡도는 모두 O(n)이 됩니다.
각 노드를 한 번씩만 방문하며, 최악의 경우 링크드 리스트의 형태의 트리가 주어져 호출 스택이 노드의 수만큼 깊어지기 때문입니다.
재귀 함수 내에서
nonlocal키워드를 사용하는 이유에 대해서는 관련 포스팅을 참고하세요.
풀이 2
FIFO(First In, First out), 즉 선입선출의 특성을 가진 자료구조인 큐(Queue)를 활용하면 어떨까요? 그러면 복잡하게 다수의 재귀 함수 호출을 넘나들며 인덱스를 지속적으로 관리해줄 필요 없겠죠?
from collections import deque
class Codec:
def serialize(self, root):
if not root:
return "N"
left = self.serialize(root.left)
right = self.serialize(root.right)
return f"{root.val},{left},{right}"
def deserialize(self, data):
values = deque(data.split(","))
def dfs():
value = values.popleft()
if value == "N":
return None
node = TreeNode(int(value))
node.left = dfs()
node.right = dfs()
return node
return dfs()