LeetCode의 212번째 문제인 Word Search II를 함께 풀어보도록 하겠습니다.
문제
글자들로 이루어진 m x n 판과 문자열의 목록인 words가 주어졌을 때, 글자판에서 있는 모든 단어를 반환하시오.
각 단어는 수평 또는 수직으로 인접한 셀들의 글자들로 만들어져야 합니다. 동일한 문자 셀은 한 단어에서 두 번 이상 사용될 수 없습니다.
예제

입력:
board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]]
words = ["oath","pea","eat","rain"]
출력: ["eat","oath"]
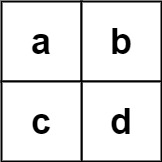
입력:
board = [["a","b"],["c","d"]]
words = ["abcb"]
출력: []
풀이 1
이 문제는 예전에 풀었던 Word Search 문제에서 구현했던 알고리즘을 그대로 가져와서 사용할 수 있습니다. 단지 차이점은 하나의 문자열 대신에 여러 문자열을 대상으로 같은 작업을 해야한다는 것입니다. 따라서 주어진 문자열 배열을 상대로 루프를 돌면서 각 문자열에 대해서 동일한 알고리즘을 적용하면 됩니다.
class Solution:
def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
def dfs(word, idx, row, col):
if idx == len(word):
return True
if not (0 <= row < len(board) and 0 <= col < len(board[0])):
return False
if board[row][col] != word[idx]:
return False
temp = board[row][col]
board[row][col] = ""
result = any(
[
dfs(word, idx + 1, row - 1, col),
dfs(word, idx + 1, row + 1, col),
dfs(word, idx + 1, row, col - 1),
dfs(word, idx + 1, row, col + 1),
]
)
board[row][col] = temp
return result
def exist(word):
for r in range(len(board)):
for c in range(len(board[0])):
if dfs(word, 0, r, c):
return True
return False
return [word for word in words if exist(word)]
입력 격자의 높이를 m, 너비를 n, 문자열의 수를 w, 문자열의 최대 길이를 s라고 했을 때, 이 풀이의 시간 복잡도는 O(m * n * w * 4^s)입니다.
문자열 하나가 격자에 존재하는지 구하는데 O(m * n * 4^s) 시간이 걸리는데 이 작업을 문자열 수인 w번 반복해야하기 때문입니다.
풀이 2
문자열을 검색하는데 최적화된 자료구조인 트라이(Trie)를 사용하면 이 문제를 좀 더 효과적으로 해결할 수 있습니다.
우선 모든 문자열을 트라이에 추가를 합니다. 그 다음에는 글자판의 각 좌표로 부터 시작해서 상하좌우를 재귀적으로 깊이 우선 탐색을 시작하는데요. 이 때 트라이도 최상위 노드부터 함께 따라 내려갑니다.
예를 들어, 다음 5개의 단어를 트라이에 저장하면 아래와 같은 모습이 되는데요.
words = ["oa", "oath", "pea", "eat", "rain"]
o
a($)
t
h($)
d
i
g($)
o
g($)
s($)
다음과 같은 글자판에서 단어를 상하좌우를 재귀적으로 깊이 우선 탐색하면 다음과 같은 모습으로 찾아질 것입니다.
board = [
["o", "a", "a", "n"],
["e", "t", "a", "e"],
["i", "h", "d", "o"],
["i", "f", "l", "g"],
]
board[0][0] = "o" 👉 트라이에 "o"로 시작하는 단어 있어서 추가 탐색
상: board[-1][0] 👉 글자판에서 벗어남 ❌
하: board[1][0] = "e" 👉 트라이에 "oaa"로 시작하는 단어 없음 ❌
좌: board[0][-1] 👉 글자판에서 벗어남 ❌
우: board[0][1] = "a" 👉 트라이에서 "oa" 찾음 ✅
상: board[-1][1] 👉 글자판에서 벗어남 ❌
하: board[1][1] = "t" 👉 트라이에 "oat"로 시작하는 단어 있어서 추가 탐색
상: board[0][1] = "a" 👉 이미 사용한 좌표의 글자 ❌
하: board[2][1] = "h" 👉 트라이에서 "oath" 찾음 ✅
좌: board[1][0] = "e" 👉 트라이에 "oate" 없음 ❌
우: board[1][2] = "a" 👉 트라이에 "oata" 없음 ❌
좌: board[0][0] = "o" 👉 이미 사용한 좌표의 글자 ❌
우: board[0][2] = "a" 👉 트라이에 "oaa"로 시작하는 단어 없음 ❌
board[2][2] = "d"
상: board[1][2] = "a" 👉 트라이에 "da"로 시작하는 단어 없음 ❌
하: board[3][2] = "l" 👉 트라이에 "dl"로 시작하는 단어 없음 ❌
좌: board[2][1] = "h" 👉 트라이에 "dh"로 시작하는 단어 없음 ❌
우: board[2][3] = "o" 👉 트라이에 "do"로 시작하는 단어 있어서 추가 탐색
상: board[1][3] = 트라이에 "doe"로 시작하는 단어 없음 ❌
하: board[3][3] = "g" 👉 트라이에서 "dog" 찾음 ✅
좌: board[2][2] = "d" 이미 사용한 좌표의 글자 ❌
우: board[2][4] 👉 글자판에서 벗어남 ❌
board[2][3] = "o" 👉 트라이에 "o"로 시작하는 단어 있어서 추가 탐색
상: board[1][3] = "e" 👉 트라이에 "oe"로 시작하는 단어 없음 ❌
하: board[3][3] = "g" 👉 트라이에 "og"로 시작하는 단어 없음 ❌
좌: board[2][2] = "d" 👉 트라이에 "od"로 시작하는 단어 없음 ❌
우: board[2][4] 👉 글자판에서 벗어남 ❌
설명드린 알고리즘을 코드로 구현해보겠습니다.
최대한 간단한 구현을 위해서 파이썬의 사전(dictionary)를 사용하여 트라이의 노드를 나타내였습니다.
각 글자를 키로 자식 사전을 값으로 저장하고, 해당 노드에서 끝나는 단어가 있다면 $ 키에 전체 단어를 저장하였습니다.
class Solution:
def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
root = {}
for word in words:
node = root
for ch in word:
if ch not in node:
node[ch] = {}
node = node[ch]
node["$"] = word
output = []
def dfs(row, col, node):
if "$" in node:
output.append(node["$"])
del node["$"] # 같은 단어를 중복해서 찾는 것을 방지
if not (0 <= row < len(board) and 0 <= col < len(board[row])):
return
if board[row][col] not in node:
return
node = node[board[row][col]]
temp = board[row][col]
board[row][col] = ""
dfs(row - 1, col, node)
dfs(row + 1, col, node)
dfs(row, col - 1, node)
dfs(row, col + 1, node)
board[row][col] = temp
for r in range(len(board)):
for c in range(len(board[r])):
dfs(r, c, root)
return output
이 풀이는 더 이상 w 번 반복을 하지 않으므로 시간 복잡도가 O(m * n * 4^s)로 개선됩니다.
마치면서
이 문제가 너무 어려우셨다면 비슷하지만 좀 더 쉬운 문제인 Word Search도 풀어보시라고 추천드립니다.